Khi nhắc đến công thức Hero, thì mình nghĩ rằng rất rất nhiều bạn đều biết về loại công thức này vì nó cực kỳ quan trọng trong toán học. Áp dụng, sử dụng nhiều trong việc tính diện tích tam giác… hay một số công thức khác. Trong bài viết này, mtrend.vn sẽ gửi đến bạn công thức Heron cùng một số bài toán liên quan tới công thức này nhé.
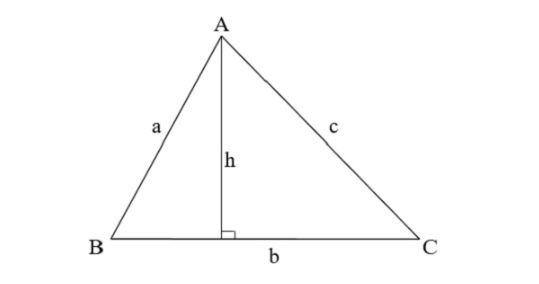
Công thức Hero là công thức tính diện tích của tam giác khi biết được độ dài của 3 cạnh.
Công thức
Gọi S là diện tích và độ dài 3 cạnh tam giác lần lượt là a, b, và c.
![]()
Với p là nửa chu vi của tam giác
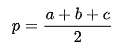
Hay còn có thể được viết theo:
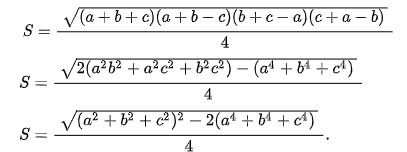
Một công thức tương đương khác
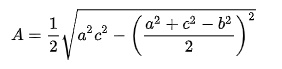
Chứng minh
Gọi a, b, c lần lượt là 3 cạnh của tam giác và A, B, C lần lượt là các góc đối diện của các cạnh
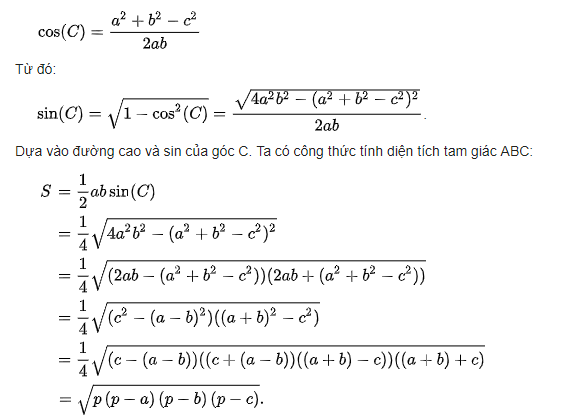
Bài tập áp dụng
a. AB = 6, BC = 10 , AC = 8
b. AB = 9, BC = 11, AC = 6
c. AB = 4a , BC = a, AC = a
Với công thức Heron trên, mọi người có thể áp dụng và dùng đến khi có những bài tập tương tự nhé.
Xem thêm:
Học Tiếng Hàn Có Khó Không Và Mẹo Học Tiếng Hàn Hiệu Quả
Bí Quyết Học Tiếng Hàn Giao Tiếp Cấp Tốc Hiệu Quả
Top 9 cầu thủ trẻ tài năng đáng xem nhất làng túc cầu hiện nay

